Einleitung

Die schiefe Beleuchtung ist ein preiswertes und einfach zu realisierendes Verfahren der Kontraststeigerung in der Mikroskopie. In der Literatur existieren verschiedene Hinweise, dass eine Theorie zu ihrer Erklärung bislang nicht existieren würde.

Die Theorie der schiefen Beleuchtung

Als Physiker mit langer Historie in der Modellierung optischer Systeme und Algorithmen zur digitalen Bildverarbeitung ruft die Aussage, eine Theorie zur Erklärung der schiefen Beleuchtung würde nicht existieren, bei mir immer ein gewisses Schmunzeln hervor. Tatsache ist, dass die schiefe Beleuchtung am Mikroskop sicherlich kein einfach zu verstehendes Phänomen ist. Andererseits hat Ernst Abbe den Begriff der äußerst schiefen Beleuchtung bereits zur Herleitung der Theorie zur mikroskopischen Auflösung mit dem Wellenmodell des Lichts verwendet. Vielfach wurden die Gedanken weiter gesponnen bis (nicht zuletzt) Max Born das mikroskopische Auflösungsvermögen mit Hilfe der Fourieroptik in seinem Lehrbuch der elektro-magnetischen Lichtwellen herleitete. Die Fourieroptik selbst begründete einen modernen Zweig der Signalverarbeitung optischer Abbildungen, die optische und digitalen Bildverarbeitung nahtlos miteinander verbindet. Deren wichtiges mathematisches Werkzeug ist die Fourier-Transformation, die mathematische Formulierung der optischen Abbildung in der Brennebene eines optischen Systems. Die Fourier-Optik hat heute viele Anwendungen in der Technik, etwa in der Mikroskopie und Astronomie.

Die elektro-magnetische Theorie der optischen Abbildung leitet die optische Auflösung des Mikroskops über ein mathematisches Modell der Abbildung mit Linsen her. Genau genommen handelt es sich um das mathematisch-physikalische Modell der Interferenz des Lichts. Dieses mathematische Modell kann heute mit einem leistungsfähigen Computer berechnet und simuliert werden. Hierzu greift man zu einem Trick und bedient sich der komplexen Zahlen, um Lichtwellen mathematisch als Schwingungen modellieren: Die Schulmathematik wird in der Post-Abbe Ära der modernen Optik auf den Kopf gestellt: Der Zahlenraum der komplexen Zahlen wird um die imaginäre Zahl "i" erweitert, die salopp ausgedrückt die Quadratwurzel aus -1 darstellt. Mit dieser mathematischen Konstruktion einer "verbotenen" Zahl, die den reellen Zahlenraum erweitert, lässt sich der Dualismus von Wellen und Teilchen (Lichtwelle versus Photonen) berechenbar gestalten. Man zerlegt die Lichtwelle in die Amplitude und einen Phasenanteil der quasi den Ausschlag der Schwingung angibt. Die Lichtwelle wird so zu einem mathematischen Vektor mit zwei Komponenten, einem realen und einem imaginären Teil. Die Lichtwelle rotiert nun in zwei Dimensionen um eine Achse, die ihre Ausbreitungsrichtung angibt. Die optische Abbildung und ihre Wellennatur der Interferenz können so mathematisch und mit dem Computer berechnet werden. Diese Berechnungen ersetzen die Vorstellung von einem Lichtteilchen und liefern eine (für den Physiker) einfacher nachvollziehbare und berechenbare Idee die Lichtausbreitung und optische Abbildungen zu beschreiben. Das Lichtteilchen (Photon) und die geometrische Optik können die Effekte der Lichtausbreitung und der optischen Abbildung ohnehin nicht vollständig erklären. Wir wollen die Theorie der elektro-magnetischen Wellen, von denen das sichtbare Licht nur einen Teil darstellt, an dieser Stelle jedoch nicht vertiefen, sondern nur Ergebnisse betrachten.

Computersimulation der schiefen Beleuchtung

Die exakte Theorie der schiefen Beleuchtung ist nicht trivial. Man muss sich die Physik der Bildgebung im Mikroskop oder das Ergebnis, aufgenommen mit unserer Digitalkamera, ein wenig näher ansehen. Mit dem Durchlicht-Mikroskop betrachten wir eigentlich dicke Objekte durch die wir hindurch sehen. Wir müssen daher einige Annahmen treffen und eine Region eingrenzen, in der unsere Modellrechnung anwendbar bleibt:

1. Das betrachtete (transparente) Objekt soll sehr dünn sein
2. Der vollständige optische Aufbau des Mikroskops mit Köhlerbeleuchtung, von der Lichtquelle, über Kondensor und Objektiv bis zur Kamera oder dem Auge, soll für die Rechnung vereinfacht werden

Die Vereinfachung des betrachteten Objekts ist gegeben, wenn wir kleine Objekte etwa Zellorganellen betrachten, deren Dicke unterhalb des axialen Auflösungsvermögen des Objektivs bleibt. Mit einem hochauflösenden Wasser-Immersionsobjektiv mit numerischer Apertur NA=1,2 lässt sich eine hohe Bildauflösung realisieren und feinste Details wiedergeben. Ein solches Objektiv besitzt eine hohe laterale Auflösung. Die axiale Auflösung ist jedoch weit schlechter und entspricht einer Schichtdicke von etwa 1 µm. Dies entspricht ungefähr der Dicke der scharf abgebildeten Bildebene. Natürlich lassen sich auch die Ränder dicker Objekte im Mikroskop kontrastieren, die theoretische Rechnung würde an dieser Stelle jedoch zu kompliziert werden. Daher betrachten wir der Einfachheit halber nur einen flachen Ausschnitt. Natürlich können Physiker manchmal sehr pragmatisch sein und  "klopfen die Objekte in notfalls gedanklich flach wie ein Schnitzel". Hier liegt der Fall jedoch anders, da beim Mikroskop aus optischen Gründen nur dünne Schichten zu betrachten sind. In diesen dünnen Schichten eines abbildenden, optischen Systems sind die Regeln der geometrischen Optik nicht anwendbar, in der Objektebene oder der Bildebene.

Die zweite Vereinfachung in der Computer-Simulation erreichen wir, indem wir den optischen Aufbau der Köhlerbeleuchtung und der resultierenden Abbildung mathematisch reduzieren. Andernfalls müssten wir mehrere Ebenen, nämlich die Ebenen der Beleuchtung, Kondensorblende, Präparateebene, Objektivblende und Bildebene betrachten. Die gesonderte Betrachtung der Kondensorblende können wir aufgrund des besonderen optischen Aufbaus der Köhlerbeleuchtung durch eine gewisse Äquivalenz von Kondensorblende und Blendenebene des Mikroskop-Objektivs reduzieren und die Manipulation hierhin verlagern. Somit reduzieren wir den Rechenaufwand. In der Vereinfachung habe ich weitere Annahmen und mathematische Korrekturen getroffen, die physikalisch gesondert diskutiert werden müssten. Es würde jedoch zu weit führen, diese Details ausführlich darzustellen oder die mathematischen Besonderheiten zu erörtern. Die Größenverhältnisse von Durchmesser der Kugel, Lichtwellenlänge oder Pixeldimension in der Simulation auf die Bildpixel zu übertragen erfordern weitere Überlegungen, die ebenfalls wesentlich für das korrekte Ergebnis sind.

Im Folgenden wollen wir solch eine kleine Kugel mit etwa 1 Mikrometer (µm) Durchmesser betrachten und deren Abbildung theoretisch mit dem Computermodell studieren. Wir nehmen ferner monochromatisches Licht von 550 nm an (gelbgrün). Der Kondensor beleuchtet im mikroskopischen Präparat unsere kleine Kugel von unten. Wir nehmen an, unsere Kugel ist transparent, schwimmt in wässriger Lösung (Brechungsindex N=1,33) und besteht aus einem anderen Material (Brechungsindex von Glyzerin, N=1,47). Damit hat die Kugel einen anderen Brechungsindex, als das umgebende Medium in dem sie schwimmt. Kleine Organellen oder Einschlüsse in der Zelle haben solche ähnlichen Eigenschaften. Ähnliches gilt für transparente Objekte, die in Harzen oder Kunstharz eingebettet werden, etwa Schalen von Kieselalgen. Das eingesetzte Objektiv sei ein hochauflösendes Objektiv mit NA=1,2, z.B. eine Wasser- oder Ölimmersion mit hoher Vergrößerung.

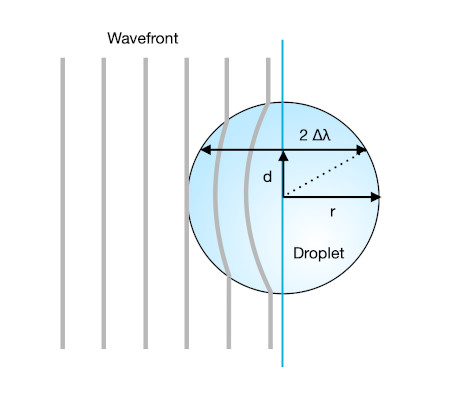
Unterschiede im Brechungsindex werden die hindurch laufende Lichtwelle in der transparenten Kugel mit anderer Geschwindigkeit und anderer Wellenlänge laufen lassen. Je nachdem, wo die Lichtwelle durch die Kugel läuft erfährt sie eine Weglängendifferenz. Hinter der Kugel, dem Beobachter zugewandt, entsteht ein Versatz der Lichtwelle, der zu einer veränderten Interferenz der ebenen Lichtwelle  führt.

Wäre keine Kugel im Sichtfeld, würden wir eine rein weiße Ebene sehen, da die Lichtwelle unverändert bleibt. Jetzt schieben wir gedanklich den Objektträger mit der kleinen Kugel unter das Objektiv und sehen uns an, was passiert. Hätte die Kugel den gleichen Brechungsindex, wie das sie umgebende Medium, würden wir sie ebenfalls nicht erkennen können.

Hat unsere Kugel nur eine geringe Absorption, und ist sie nicht gefärbt, werden wir diese Erscheinungen nur schwer im Durchlicht erkennen. Die Wellenfront ist jedoch innerhalb der Kugel etwas abgelenkt durch den unterschiedlichen Brechungsindex. Dies führt dazu, dass die Lichtwellen geringfügig abgelenkt werden dort, wo sie die Kugel durchlaufen. Durch die Beugung am Rand des Mikroskopobjektiv wird nun die Auflösung begrenzt. Genau genommen ist Beugung am Objektiv physikalisch auch nur eine spezielle Form der Interferenz, nämlich ein Bandpassfilter oder ein Kantenfilter. Daher muss ich im weiteren Text auch nicht zwischen Beugung und Interferenz unterscheiden.

Interferenz der gestörten Lichtwelle erzeugt nun in der Bildebene ein Abbild unserer Kugel. Dieses Bild ist jedoch kaum wahrnehmbar und besitzt nur einen geringen Kontrast. Die Kugel fällt lediglich dadurch auf, dass eine schwach wahrnehmbare Interferenzerscheinung ihren Rand abgrenzt. Der dunkelste Interferenzring definiert den äußeren Durchmesser unserer kleinen Kugel. Die Kugel absorbiert nur wenig Licht und besitzt eine Transparenz von 98%. Ein solch transparentes Objekt ergibt nicht viel Kontrast im Durchlicht, im Gegenteil. Das einzige, was wir von ihr sehen ist eine schwache Interferenz auf einem weißen Hintergrund.

Man muss das Sehen im Mikroskop sicherlich auch erlernen. Jedoch ist die unveränderte Hellfeldbeleuchtung sicherlich die schlechteste Möglichkeit ein nicht gefärbtes, transparentes Objekt im mikroskopischen Präparat im Durchlicht zu betrachten. Dies ist der mathematische Beweis mit Hilfe einer Computersimulation.

Viele Mikroskope besitzen einen Kondensor der verschiedene Blenden für Hellfeld und Phasenkontrast besitzt. Hier kann man die Hellfeldblende etwas herausdrehen. Diese Praxis habe ich hier etwas ausführlicher beschrieben. Der Kondensor leuchtet das Präparat nun "schief" aus, das heißt nur einseitig beleuchtet. Wir kontrollieren die Einstellung, indem wir das Okular herausnehmen und von hinten auf das Objektiv blicken. Das Präparat wird jedoch nicht wirklich schief durchleuchtet, es ist immer noch eben ausgeleuchtet. In unserem theoretischen Modell kann man dies natürlich sehr exakt einstellen, wie im folgenden Bild dargestellt:

Violá, unsere Kugel ist nun viel besser zu sehen. Doch, wie ist das möglich?

Die halbseitige, schiefe Ausleuchtung führt dazu, dass ein großer Teil der Lichtwellen unser transparentes Objekt nicht mehr passieren wird, denn wir haben verhindert, dass dieses Licht die Mikroskopoptik durchläuft. Es fehlen quasi Lichtwellen mit einem bestimmten Vorzeichen auf der rechten Seite unserer Kondensorblende.

In der Folge fehlen diese Anteile nun auch in der Rekonstruktion der Abbildung hinter dem Objektiv. Wir haben die Lichtintensitäten durch Manipulation der Lichtwelle "umgeschichtet". Hell zur einen, dunkel zur anderen Seite. Dadurch erscheint die Kugel plötzlich reliefartig kontrastiert. Auch wenn dies eine nahe liegende Erklärung wäre, entsteht jedoch kein echter Schattenwurf. Die Effekte des Lichts spielen sich hier in der Größenordnung der Lichtwellenlänge ab. Die betrachtete Kugel von 1 µm Durchmesser misst hier gerade einmal die doppelte Lichtwellenlänge. Dies ist, was Abbe meinte, als er in seiner ursprünglich auf englisch verfassten Arbeit schrieb:

Ernst Abbe und Zeitgenossen war durchaus bewusst, dass wir es mit Wellenphänomenen und nicht mit "geometrisch schiefen" Lichtstrahlen zu tun haben. Daher sehen wir keine echten Schatten, sondern Interferenzphänomene. Unser Computermodell hat eine Interferenzanalyse berechnet. Es wurde eine Summe der Licht-Teilwellen auf allen Wegen, die noch vorhanden sind, gebildet, mit dem Ergebnis, dass sich das Interferenz-Bild im Auge oder auf dem Kamerasensor verändert. Der Reliefkontrast entsteht durch Verlagerung der teilweisen Auslöschung oder Verstärkung der interferierenden Lichtwellen im Bild. Einige Teilwellen wurden quasi ausgesperrt. Die noch vorhandenen Lichtwellen werden sich durch Interferenz in der Bildebene nun auf andere Weise verstärken oder gegenseitig auslöschen. Die schiefe Beleuchtung ist also ein reinrassiges Interferenzkontrast-Verfahren.

Rocket Science oder Welle-Teilchen-Dualismus?

Hat man einige Erfahrung mit der Einstellung der schiefen Beleuchtung und der Betrachtung der winzigen Objekte, während man den Fokusknpf am Mikroskop bedient, so fällt dem Physiker noch auf, dass die mit der Kamera aufgenommenen Interferenzerscheinungen typischerweise geringfügig anders ausfallen, als das theoretische Modell dies im ersten Anlauf vorhersagt. Eher muss man sich bemühen, das Bild genau so aussehen zu lassen, wie vorhergesagt. Dieses Problem liegt ursächlich darin begründet, dass wir mit der Hand am Fokusknopf eine andere Vorstellung haben, wie die betrachteten Zellorganellen aussehen sollten! Das physikalische Modell lässt sich mit einer kleinen Modifikation natürlich auch um die Hand des Beobachters am Fokusknopf erweitern, um diese Effekte darzustellen.

Man ist intuitiv versucht, der gedachten Kugelform eine andere Plastizität zu geben. Mit anderen Worten: Theorie und reale Abbildung klaffen auseinander, weil der Mikroskopiker den Fokus intuitiv in eine andere Ebene verlagert, in der die Kugel "nach eigenem Ermessen" entweder besser kontrastiert oder harmonischer ausgeleuchtet erscheint. Die Beobachtung, dass der Bildeindruck der beobachteten Interferenzerscheinungen je nach Fokuslage sogar hin und her springen kann, ist das wohl wichtigste Indiz dafür, dass wir es mit dem Phänomen der Interferenz des Lichts zu tun haben und nicht mit einer "geometrisch schief erklärten Schattenbildung".

Die schiefe Beleuchtung ist ziemlich kompliziert zu verstehen und unterliegt obendrein der subjektiven Einschätzung des Beobachters selbst. Alle Theorie ist grau und hat ihre natürlichen Grenzen in der menschlichen Tendenz der Natur ein "ganz persönliches, natürliches Ideal" voran zu stellen. Selbst der Physiker kann sich, wenn er kreativ ist, davon nicht frei sprechen und wird dummerweise genau an dieser Stelle subjektiv in seiner Beurteilung des ästhetischen Eindrucks. Dies verlangt natürlich noch nach einer erweiterten Theorie der schiefen Beleuchtung.

Die schiefe Beleuchtung ist keine Rocket-Science. Im Gegenteil, sie ist trotz ihrer einfachen Theorie zweifellos noch komplizierter, als Rocket Science. Nur wenige haben sie je richtig verstanden. Armes Kind. Aber wir wissen ja auch, dass man den wahren Weg eines Lichtteilchen nicht beobachten kann. Würden wir es können, wird es sich anders verhalten. Licht kann ein sehr trotziges Kind sein. Ein (vorläufig) philosophischer Notausgang im Verständnis der schiefen Beleuchtung.

In diesem Sinne wünsche ich viel Spaß beim Experimentieren mit der schiefen Belechtung!

Literatur

• Abbe E. On the Estimation of Aperture in the Microscope. J R Microsc Soc. 1881; 1: 388-423.
• Bauer T. Die perfekte schiefe Beleuchtung. Mikroskopie 4/2020. Dustri Verlag.
• Berek M. Über Kohärenz und Konsonanz des Lichtes. Z Phys. 1927; 40: 420-450.
• Born M. Optik. Ein Lehrbuch der elektro-magnetischen Lichttheorie, Berlin: Springer; 1981; Nachdruck der 3. Auflage, S. 182ff.
• Goodman JW. Introduction to Fourier Optics. 3rd Edition. Greenwood Village: Roberts & Company Publishers; 2004.